Концы данного отрезка, не пересекающего плоскость, удалены от нее на 30 см и 50 см. Как удалена

RomQa_ · Форумчанин Предупреждений : 1

Концы данного отрезка, не пересекающего плоскость, удалены от нее на 30 см и 50 см. Как удалена от плоскости точка, делящая данный отрезок в отношении 3:7? (Два случая)

Wizenya · Гуру

30+(50-30)*3/7
30-(50-30)*(7-3)/7 - это если точка в другой стороне

RomQa_ · Форумчанин Предупреждений : 1

Извините,а можно расширить совй ответ,на основании чего так решили)

Wizenya · Гуру

эта точка не может быть ближе 30 и дальше 50 от плоскости. Начерти и подсчитай. Я просто в уме это решил.

RomQa_ · Форумчанин Предупреждений : 1

хахаххах))))) ну это понятно)
просто я не понимаю ход решения,мне же оформить надо как-то

ДобрыйФей · Мечтатель Предупреждений : 5

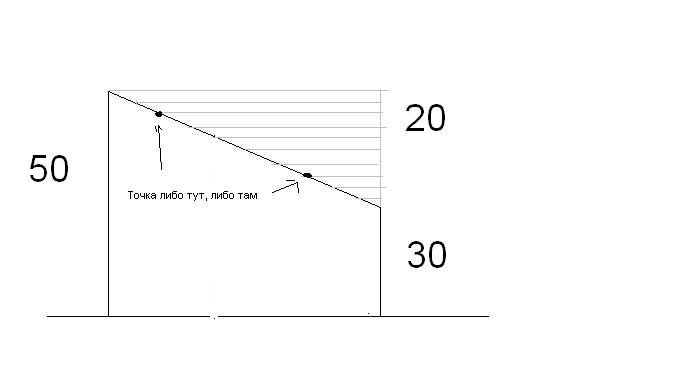
Пусть эта убогая картинка будет иллюстрацией.
Суть в том, что

RomQa_ · Форумчанин Предупреждений : 1

Ага))))спасибо))
А можете еще помочь с задачкрй одной:
отрезки двух прямых, заключенных между параллельными плоскостями равны 51 см и 53 см, а их проекции на одну из плоскостей относятся как 6:7. Найти расстояние между данными плоскостями.

ДобрыйФей · Мечтатель Предупреждений : 5

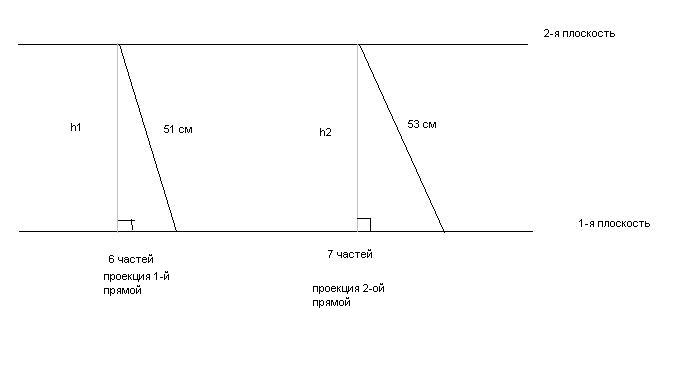
Опять рисунок.
2 треугольника на рисунке - прямоугольные, т.к. h1 и h2 - это расстояние между плоскостями, а расстояние - это перепендикуляр.
Опять же, 6:7 означает, что в первой проекции содержится 6 одинаковых частей, а во второй - 7 таких же.
Пусть 1 такая часть - это х, тогда проекция первой прямой - 6*х, а второй - 7*х.
По теореме Пифагора:
51*51=6*х*6*х+h1*h1 и 53*53=7*х*7*х+h2*h2.
Но h1=h2, т.к. плоскости параллельны, а h1 и h2 - расстояния между ними.
h1=h2=h. Тогда:
51*51=6*х*6*х+h*h и 53*53=7*х*7*х+h*h.
h*h=51*51-6*х*6*х и h*h=53*53-7*x*7*x.
Левые части равны, приравняем правые.
51*51-6*х*6*х=53*53-7*x*7*x.
Отсюда ищется х, потом подставляется в любое из уравнений, например, в h*h=53*53-7*x*7*x. Находится h - это ответ задачи.

RomQa_ · Форумчанин Предупреждений : 1

ну блин))))спасибо)выручил)

Wizenya · Гуру

Он Фей. Он Добрый...